열 전달에 관한 공식을 유도하고, 필요한 정보를 나열하겠습니다.
두 개의 물체 사이에 온도차가 있으면 고온물체로부터 저온물체로 열이 이동하는데, 금속의 경우 한 끝을 가열하면 물질 매체 내부에서 높은 병진운동에너지를 가진 분자로부터 낮은 병진운동에너지의 인접분자로 열이 전달되는 과정을 물질자체의 이동 없이 수행됩니다. 이것을 전도(conduction)현상이라고 합니다.
유체(액체, 기체)에서는 매질 속의 높은 온도를 가진 부분이 낮은 온도를 가진 부분으로 물질자체가 이동하면서 열이 전달되는 대류(convection)과정이 일어납니다.
길이 L의 금속막대의 좌단은 온도 T1의 뜨거운 물체에, 우단은 온도 T2의 차가운 물체에 접촉시켰을 때 좌측의 큰 병진운동에너지가 옆의 분자에게 에너지를 전달해 나갑니다. 시간이 경과하면서 막대 내의 온도 분포가 변하지 않는 정상 상태(steady state)가 됩니다.
이때 막대의 단면적을 통해서 흐르는 열량을 계산하고자 합니다. 임의의 단면적 A를 통과하는 열량 ΔQ는 단면적 A, 온도차 ΔT, 시간 Δt에 비례하며 두께 Δx에 반비례합니다. 즉,
ΔQ /Δt =-k A(ΔT/Δx) , 단 k는 비례상수로서 그물질의 열전도율(thermal conductivity)이라고 부릅니다. ΔQ /Δt 는 임의의 단면적을 통해 흐르는 열류의 흐름율로서 열흐름율 H 이라고 합니다.
ΔT/Δx는 온도기울기(temperature gradient)라고 부르며 막대 길이 방향에서 x에 따라 온도의 변화율을 나타냅니다.
금속에 있어서의 열전도율(열 전달율) k는
k=-(ΔQ /Δt) / ( A(ΔT/Δx) ) cal/s-cm-℃, Kcal/s-m-℃, Btu-in/s-ft2-F°
알루미늄 0.49, 놋쇠 0.26, 구리 0.92, 은 0.97, 강철 0.11로 알려져 있습니다.
열흐름율 H는
H=ΔQ /Δt = k A(T1-T2)/L
파이프(직경 D cm) 안에 있는 물체(질량 m)를 가열하기 위해서 파이프와 물체에 유체를 흘려주려 할 때, 한 끝은 T1이 되고 다른 끝은 T2가 될 것입니다. 몇 ℃의 유체를 얼마나 흘려주어야 되는지 계산하기 전에 열 대류에 의한 열 손실을 살펴볼 필요가 있습니다.
열풍로, 증기라디에이터, 온수난방 장치 등은 온도가 매우 높지 않은 유체의 열전달의 주요 방법인 대류를 이용한 것입니다. 유체의 일부분이 고온T1 에서 저온T2 으로 직접 이동하는 것입니다. 열의 증감현상은 표면의 기하학적 모양, 유체의 특성인 밀도, 비열, 열전도도, 점성등과, 유선형흐름인가 난류인가에 의존하게 됩니다.
이 때 H는 임의의 면적을 통해서 단위시간에 흐르는 열이라 할 때
H = h A' (T1-T2), h는 대류계수(convection coefficient)이며 단위면적의 표면에서 단위시간당 단위온도차당 증감하는 열을 의미합니다. h의 단위는 cal/s-cm2-℃, Kcal/s-m2-℃등입니다.
직경 D 의 수평 또는 수직하게 놓인 파이프에서 대기압에서의 자연대류에 대한 h의 값은 실험에 의해 Newton의 냉각법칙(Newton's law of cooling)에 따른다는 것이 알려져 있습니다. 곧,
h=1.00 . 10-4(ΔT/D)1/4 cal/s-cm2-℃, ΔT는 관 내외부의 온도차
한 물체가 주위의 공기에 열을 상실하는 속도는 그들의 온도차가 매우 크지 않는 한 그들의 온도차에 직접 비례하며, 이때 대부분은 대류에 의해 열이 전달되며 전도 및 복사과정은 극히 미소하다는 것입니다.
따라서 대류에 의해 시간당 상실하는 열Q'은 다음처럼 계산 됩니다.
관이 공기에 접하는 부분의 표면적은 A'=2πrL, 수평 관(D=2r)에 대해서
h= 1.00 . 10-4(ΔT/D)1/4
H = h A' (T1-T2)= 1.00 . 10-4(ΔT/2r)1/4 2πrL (ΔT)
= πL. 1.00 . 10-4(ΔT)5/4 (2r)3/4
Q'= HΔt =πLΔt .1.00 . 10-4(ΔT)5/4 (2r)3/4 = π(2)3/4 10-4 . (r)3/4 (T1-T2)5/4 L Δt
의 열 손실이 있게 됩니다.
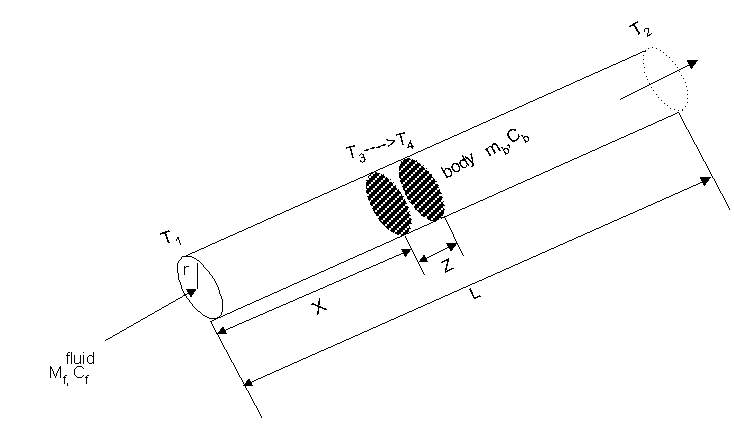
파이프(직경 D cm) 안에 있는 물체(질량 m 길이 z )를 가열(온도를 T3에서 T4로 높여줌)하기 위해서 파이프와 물체에 유체를 흘려주려 할 때, 관의 한 끝은 T1이 되고 관의 다른 끝은 T2가 될 것입니다. T1 ℃의 유체를 얼마나(Mf) 흘려주어야 되는지 계산하기로 합니다.
만일 관 안의 물체가 위치 X 인 지점에 놓여 있다면, 유체가 물체에 닿을 때까지의 열 손실은
Q' = π(2)3/4 10-4 . (r)3/4 (T1-T3)5/4 Δt x 이므로, 처음 유체의 온도 T1 ℃ 는 T4 로 낮아지고, 관 안의
물체는 처음온도 T3 에서 T4로 올라갈 것입니다. 그리고 물체(길이 z)를 통과한 유체는 남은 관 길이(L-x-z) 을 지나는 동안 또 한 번의 열 손실을 가져오고 관의 다른 끝에서 온도T2가 될 것입니다.
열손실을 제외하고, 유체(fluid)가 잃은 열량은 관 안의 물체(body)가 얻은 열량이 될 것 입니다. 즉,
Mf Cf (T1-T4) -Q'X- Mb Cb (T4-T3) - Q'(L-X-z)= Mf Cf (T4-T2 )
계산하여 정리하면 (마우스를 클릭하시면 선명하게 보입니다.) 식과 그림.
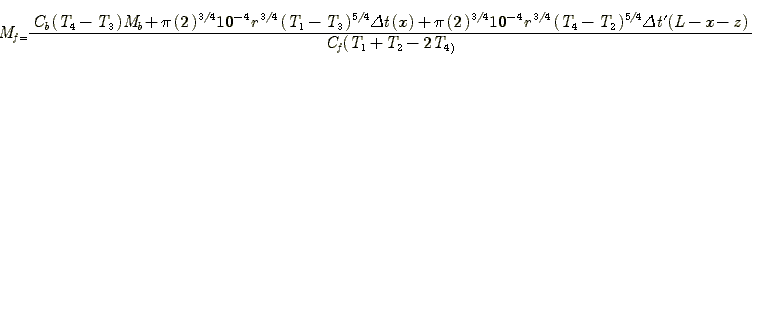
파이프 - 재질:s.s 304 size:1/2" Sch10s
물체 - 재질:A351 CF8M size: 환봉Φ84-125L 온도: 100 ℉ 희망온도: 200 ℉
유체 - 물
에 대하여 제가 아는 정보는 아래와 같습니다. 재질의 명칭과 단위를 감안하셔서 아래(?)에 대입하고서 계산하시면 됩니다.
Tc= (5/9)(TF-32)℃, T3=100 ℉= 340/9 ~37.777 ℃, T4= 200 ℉ = 840/9~93.333 ℃
파이프 직경 D=2r = 1/2'= 1.27cm, Sch10s=외경 2.17cm, 두께 0.21cm길이=?
Mf = 물의 질량 = 구하고자 하는 양 , Cf = 1,
Mb = A351 CF8M 질량 = ? Kg
Cb = A351 CF8M 비열 = 0.12 cal/g℃
물체 길이 Z = 환봉Φ84-125L의 길이 = 125 cm
X = 파이프 내에서 물체의 놓인 위치= ?cm
Δt = 물이 파이프 입구에서 물체까지 가는 시간= ? (sec)
Δt‘= 물이 물체에서 파이프 출구가지 가는 시간= ? (sec)
'사람과 일' 카테고리의 다른 글
| 보일러 급수처리 (0) | 2007.09.04 |
|---|---|
| 보일러의 종류및 특성 (0) | 2007.08.14 |
| 열교환기의 전열면적 구하기 (0) | 2007.08.14 |
| 도움되는 수치 변환표 (0) | 2007.08.04 |
| 주강의 종류와 용도 (0) | 2007.06.28 |